细说浮点数

一.什么是浮点数

​ 浮点数能够表示带小数部分的数字，如我们小学常定义的Π值3.1415926，它们提供的值范围也更大也更为精准。当然如果数字很大，以至于无法表示为long类型，如人体的细菌数（估计超过100兆），则可以使用浮点类型来表示。

​ 使用浮点类型可以表示诸如2.5、3.14159和122442.32这样的数字，即带小数部分的数字。计算机将这样的值分成两部分存储。一部分表示值，另一部分用于对值进行放大或缩小。下面打个比方。对于数字34.1245和34124.5，它们除了小数点的位置不同外，其他都是相同的。可以把第一个数表示为0.341245（基准值）和100（缩放因子），而将第二个数表示为0.341245（基准值相同）和10000（缩放因子更大）。缩放因子的作用是移动小数点的位置，术语浮点因此而得名。C++内部表示浮点数的方法与此相同，只不过它基于的是二进制数，因此缩放因子是2的幂，不是10的幂。幸运的是，初学计算的程序员不必详细了解内部表示（当你学过计组之后就会有详细的认识）。重要的是，浮点数能够表示小数值、非常大和非常小的值，它们的内部表示方法与整数有天壤之别。

二.浮点数的书写

​ 在c++中浮点数分两种写法：

• 标准小数点的写法（我们常见的小数写法）

  3.14
  100.45
  99.1
  1.0

• E表示法（类似于我们常见的科学计数法）

  3.14e3//表示3.14*10^3
  3.14e+3//表示3.14*10^3
  9.11e-31//表示9.11*10^(-31)电子质量，单位千克

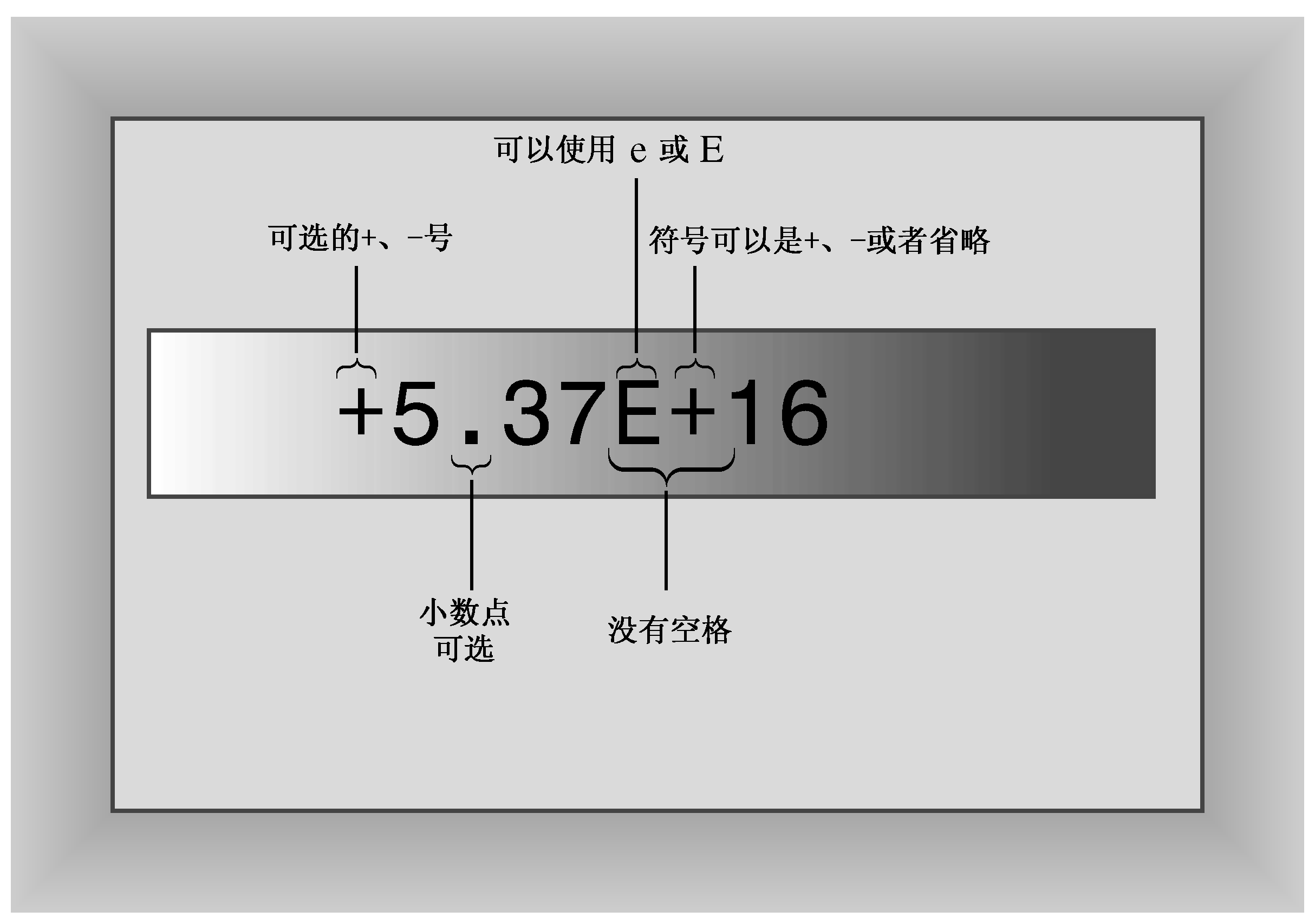
三.浮点数的分类

​ 和ANSI C一样，C++也有3种浮点类型：float、double和long double。这些类型是按它们可以表示的有效数位和允许的指数最小范围来描述的。有效位（significant figure）是数字中有意义的位。例如，珠穆朗玛峰的高度是8,849米，该数字使用了4个有效位，指出了最接近的高度数。然而，将珠穆朗玛峰的高度写成约8800米时，有效位数为2位，因为结果经过四舍五入精确到了百位。在这种情况下，其余的2位只不过是占位符而已。有效位数不依赖于小数点的位置。例如，可以将高度写成8.849米。这样仍有4个有效位，因为这个值精确到了第4位。

​ 事实上，C和C++对于有效位数的要求是，float至少32位，double至少48位，且不少于float，long double至少和double一样多。这三种类型的有效位数可以一样多。然而，通常，float为32位，double为64位，long double为80、96或128位。另外，这3种类型的指数范围至少是−37到37。可以从头文件cfloat或float.h中找到系统的限制。以下是float.h的部分代码，关键位置标有中文注

//
// float.h
//
//      Copyright (c) Microsoft Corporation. All rights reserved.
//
// Implementation-defined values commonly used by sophisticated numerical
// (floating point) programs.


// Define the floating point precision used.定义使用的浮点精度
/*
FLT_EVAL_METHOD 用来指明在表达式求值（尤其是数学运算）过程中是否需要提升浮点数的类型，可能的取值有：
    -1：未知的，不确定的。

    0：不提升类型，使用当前的类型。

    1：将浮点数提升到 double 类型，大于等于 double 类型的保持不变；也就是说，将 float 类型提升为 double 类型，double 和 long double 类型不变。

    2：将浮点数提升到 long double；也就是说，将 float、double 提升到 long double 类型，long double 类型保持不变。

	【注】FLT_EVAL_METHOD 对所有浮点数类型（float、double 和 long double）都有效，也就是说，所有浮点数类型都必须采用相同的类型提升。提升类型能够提高浮点数的精度，让表达式的结果更加精确。
*/

#ifdef _M_FP_FAST
    #define FLT_EVAL_METHOD -1
#else
    #ifdef _M_IX86
        #if _M_IX86_FP >= 2
            #define FLT_EVAL_METHOD 0
        #else
            #define FLT_EVAL_METHOD 2
        #endif
    #else
        #define FLT_EVAL_METHOD 0
    #endif
#endif


//-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
//
// Constants 定义了各种类型的数据的精度，即小数点的位数
//
//-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+



    //DBL开头的是double类型的
#define DBL_DECIMAL_DIG  17                      // # of decimal digits of rounding precision
    /*
    从 float/double/long double 转换到至少有 FLT_DECIMAL_DIG/DBL_DECIMAL_DIG/LDBL_DECIMAL_DIG 位数字的十进制，再转换回原类型为恒等转换：这是序列化/反序列化浮点值所要求的十进制精度。分别定义为至少 6、10 和 10，对于 IEEE float 为 9，对于 IEEE double 为 17。
    */
#define DBL_DIG          15                      // # 转换成十进制形式后，小数点后精确数字（能够保证精度的数字）的位数。
#define DBL_EPSILON      2.2204460492503131e-016 // smallest such that 1.0+DBL_EPSILON != 1.0 1和大于1的最小浮点数的差值，可以表示最小的有效数字
#define DBL_HAS_SUBNORM  1                       //指明类型是否支持非正规数值
    /*
    -1: 为不确定，
    0:  为不支持，
    1:  为支持。
    */
#define DBL_MANT_DIG     53                      // # of bits in mantissa
    // 基数（进制）为 FLT_RADIX 时，尾数 mantissa 的最大长度（最大位数），也可以说是浮点数的精度。注意，这里所说的长度包含了整数部分和小数部分。
#define DBL_MAX          1.7976931348623158e+308 // max value 基数（进制）为 FLT_RADIX 时，规格化浮点数的指数（也即 exponent）的最大值（为正数）。
#define DBL_MAX_10_EXP   308                     // max decimal exponent 转换为10进制后，规格化浮点数的的指数的最大值
#define DBL_MAX_EXP      1024                    // max binary exponent double指数最大二进制
#define DBL_MIN          2.2250738585072014e-308 // 定义了双精度浮点数的最小值
#define DBL_MIN_10_EXP   (-307)                  // 转换成十进制形式后，规格化浮点数的指数的最小值（为负数）。
#define DBL_MIN_EXP      (-1021)                 // 基数（进制）为 FLT_RADIX(此时为2)时，规格化浮点数的指数(也即exponent)的最小值(为负数)
#define _DBL_RADIX       2                       // exponent radix 指数的进制
#define DBL_TRUE_MIN     4.9406564584124654e-324 // min positive value 双精度浮点数的最小值
    
    
    
    //FLT开头的是float类型的，各种变量的含义同double
#define FLT_DECIMAL_DIG  9                       // # of decimal digits of rounding precision
#define FLT_DIG          6                       // # of decimal digits of precision
#define FLT_EPSILON      1.192092896e-07F        // smallest such that 1.0+FLT_EPSILON != 1.0
#define FLT_HAS_SUBNORM  1                       // type does support subnormal numbers
#define FLT_GUARD        0
#define FLT_MANT_DIG     24                      // # of bits in mantissa
#define FLT_MAX          3.402823466e+38F        // max value
#define FLT_MAX_10_EXP   38                      // max decimal exponent
#define FLT_MAX_EXP      128                     // max binary exponent
#define FLT_MIN          1.175494351e-38F        // min normalized positive value
#define FLT_MIN_10_EXP   (-37)                   // min decimal exponent
#define FLT_MIN_EXP      (-125)                  // min binary exponent
#define FLT_NORMALIZE    0
#define FLT_RADIX        2                       // 定义了浮点数的进制，对所有的浮点数都有效，所有的浮点数都必须采用2进制
#define FLT_TRUE_MIN     1.401298464e-45F        // min positive value
    
    
    
    //开头的是double long类型的，各种变量的含义同double
#define LDBL_DIG         DBL_DIG                 // # of decimal digits of precision
#define LDBL_EPSILON     DBL_EPSILON             // smallest such that 1.0+LDBL_EPSILON != 1.0
#define LDBL_HAS_SUBNORM DBL_HAS_SUBNORM         // type does support subnormal numbers
#define LDBL_MANT_DIG    DBL_MANT_DIG            // # of bits in mantissa
#define LDBL_MAX         DBL_MAX                 // max value
#define LDBL_MAX_10_EXP  DBL_MAX_10_EXP          // max decimal exponent
#define LDBL_MAX_EXP     DBL_MAX_EXP             // max binary exponent
#define LDBL_MIN         DBL_MIN                 // min normalized positive value
#define LDBL_MIN_10_EXP  DBL_MIN_10_EXP          // min decimal exponent
#define LDBL_MIN_EXP     DBL_MIN_EXP             // min binary exponent
#define _LDBL_RADIX      _DBL_RADIX              // exponent radix
#define LDBL_TRUE_MIN    DBL_TRUE_MIN            // min positive value

#define DECIMAL_DIG      DBL_DECIMAL_DIG



//定义了浮点数的舍入方式
/*
由下列代码可知，每种浮点数舍入方式是必须相同的，均是由__fpe_flt_rounds()函数确定的，不同的返回值，代表的含义如下
-1、不确定：即舍入方式不确定

1、就近舍入：

	即十进制下的四舍五入。但是也会出现以下几种情况：

	多余数字是1001，它大于0.5，故最低位进1。
	多余数字是0111，它小于0.5，则直接舍掉多余数字。
	多余数字是1000，正好是等于0.5的特殊情况；那么此时最低位为0则舍掉多余位，最低位为1则进位1。
	注意这里说明的数位都是指二进制数。因为这是尾数，所以在计算这些二进制和0.5的关系的时候，也即转为10进制的时候，我们用每一位的权重乘以2^(-i)然后求和即可。

2、朝0舍入：即朝数轴零点方向舍入，所以我们直接截尾即可。

3、朝正无穷舍入：对正数而言，多余位全为0则直接截尾，不全为0则向最低有效位进1；负数的话不管多余位是多少直接截尾即可。

4、朝负无穷舍入：对负数而言，多余位全为0则直接截尾，不全为0则向最低有效位进1；正数的话不管多余位是多少直接截尾即可。
*/

#define FLT_ROUNDS   (__fpe_flt_rounds())
#define _DBL_ROUNDS  FLT_ROUNDS
#define _LDBL_ROUNDS _DBL_ROUNDS



//-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
//
// IEEE Recommended Functions IEEE(电气电子工程师学会) 推荐的一些浮点型的常用方法
//
//-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
/*copysign()函数是cmath标头的库函数，用于获取带有第二个参数的符号的第一个参数的值，它接受两个参数( x，y )并以y的符号返回x的大小。*/
_Check_return_ _ACRTIMP double __cdecl _copysign(_In_ double _Number, _In_ double _Sign);
//返回一个与 _X 符号相反数值相同的数（正变为负，负变为正）；
_Check_return_ _ACRTIMP double __cdecl _chgsign(_In_ double _X);
//输出x乘以2的y次幂的结果；
_Check_return_ _ACRTIMP double __cdecl _scalb(_In_ double _X, _In_ long _Y);
// 求输入数是2的多少次幂，返回值对确切结果向0取整；
_Check_return_ _ACRTIMP double __cdecl _logb(_In_ double _X);
// 输出x对y方向在double精度上的下一个值；
_Check_return_ _ACRTIMP double __cdecl _nextafter(_In_ double _X, _In_ double _Y);
//检查输入是否有效，若为 INT 或 NaN 则返回0，有效数值返回1；
_Check_return_ _ACRTIMP int    __cdecl _finite(_In_ double _X);
//返回输入是否为 NaN。
_Check_return_ _ACRTIMP int    __cdecl _isnan(_In_ double _X);
    /*
    返回一个浮点数的分类，具体如下：
    _FPCLASS_SNAN	信号 NaN
    _FPCLASS_QNAN	安静的南
    _FPCLASS_NINF	负无穷大 ( -INF)
    _FPCLASS_NN	负归一化非零
    _FPCLASS_ND	负非规范化
    _FPCLASS_NZ	负零 (-0)
    _FPCLASS_PZ	正 0 (+0)
    _FPCLASS_PD	正反规格化
    _FPCLASS_PN	正归一化非零
    _FPCLASS_PINF	正无穷大 ( +INF)
    */
_Check_return_ _ACRTIMP int    __cdecl _fpclass(_In_ double _X);

#ifdef _M_X64
    _Check_return_ _ACRTIMP float __cdecl _scalbf(_In_ float _X, _In_ long _Y);
#endif


_CRT_END_C_HEADER
_UCRT_RESTORE_CLANG_WARNINGS
#pragma warning(pop) // _UCRT_DISABLED_WARNINGS
#endif // _INC_FLOAT

四.浮点数的“四舍五入”

​ 在浮点数的舍入问题上，IEEE 浮点格式定义了 4 种不同的舍入方式，如下表所示。其中，默认的舍入方法是向偶数舍入，而其他三种可用于计算上界和下界。

下表是 4 种舍入方式的应用举例。这里需要特别说明的是，向偶数舍入（向最接近的值舍入）方式会试图找到一个最接近的匹配值。因此，它将 1.4 舍入成 1，将 1.6 舍入成 2，而将 1.5 和 2.5 都舍入成 2。

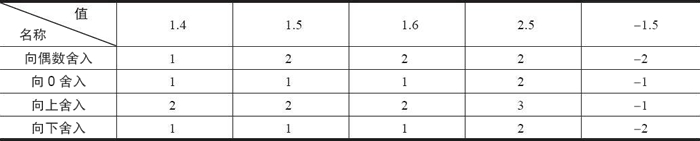
​ 或许看了上面的内容你会问：为什么要采用向偶数舍入这样的舍入策略，而不直接使用我们已经习惯的“四舍五入”呢？

​ 其原因我们可以这样来理解：在进行舍入的时候，最后一位数字从 1 到 9，舍去的有 1、2、3、4；它正好可以和进位的 9、8、7、6 相对应，而 5 却被单独留下。如果我们采用四舍五入每次都将 5 进位的话，在进行一些大量数据的统计时，就会累积比较大的偏差。而如果采用向偶数舍入的策略，在大多数情况下，5 舍去还是进位概率是差不多的，统计时产生的偏差也就相应要小一些。

​ 同样，针对浮点数据，向偶数舍入方式只需要简单地考虑最低有效数字是奇数还是偶数即可。例如，假设我们想将十进制数舍入到最接近的百分位。不管用哪种舍入方式，我们都将把 1.2349999 舍入到 1.23，而将 1.2350001 舍入到 1.24，因为它们不是在 1.23 和 1.24 的正中间。另一方面我们将把两个数 1.2350000 和 1.2450000 都舍入到 1.24，因为 4 是偶数。

五.浮点数标准IEEE754

1.IEEE浮点数标准简介

​ IEEE 于 1987 年推出了与底数无关的二进制浮点运算标准 IEEE 854，并于同年被美国引用为 ANSI 标准。1989 年，国际标准组织 IEC 批准 IEEE 754/854 为国际标准 IEC 559：1989。后来经修订后，标准号改为 IEC 60559。现在，几乎所有的浮点处理器完全或基本支持 IEC 60559。同时，C99 的浮点运算也支持 IEC 60559。

​ IEEE 浮点数标准是从逻辑上用三元组{S，E，M}来表示一个数 V 的，即 V =（-1)^S * M * 2^E，如下图所示：

• 符号位S（sign）:S = 0: 表示该数为正数，S = 1:表示该数为负数
• 指数位E（Exponent）:在计算机中用移码表示，表示2的多少次幂
• 有效位M（Significand）：在计算机中用补码表示，表示二进制小数，也称尾数

2.IEEE754标准下的浮点数的格式

补：原码，反码，补码，移码（以8位为例）

二进制整数都是以补码形式出现的。

• 正数的补码与反码、原码一致，
• 负数的补码是反码+1.这样使减法运算可以使用加法器实现，符号位也参与运算;
• 移码与补码就是符号位取反

十进制原码	二进制原码	反码	补码	移码
-128	无	无	1000 0000	0000 0000
-127	1111 1111	1000 0000	1000 0001	0000 0001
-126	1111 1110	1000 0001	1000 0010	0000 0010
……	……	……	……	……
-1	1000 0001	1111 1110	1111 1111	0111 1111
-0	1000 0000	1111 1111	无	无
+0	0000 0000	0000 0000	0000 0000	1000 0000
+1	0000 0001	0000 0001	0000 0001	1000 0001
……	……	……	……	……
+126	0111 1110	0111 1110	0111 1110	1111 1110
+127	0111 1111	0111 1111	0111 1111	1111 1111

移码的计算方法：

​ 移码 = 真值+偏置值

偏置值的计算方法

偏置值	ieee754偏置值	普通偏置值
计算方法	2^(n-1) - 1	2^(n-1)
n代表的含义	表示移码的位数	原码的位数

​ 在IEEE754标准中，规格化的浮点数的尾数部分通常隐藏最高有效位1

数符	阶码部分，使用移码表示（阶码全1或全0特殊用途）	尾数部分，用原码表示（隐藏最高位为1）
A	E	M（1.M）

​ 各类浮点数各部分占用位数及格式：

类型	大小（B)	数符	阶码	尾数	总位数（bit）	16位偏置	10位偏置
float	4	1	8	23	32	7FH	127
double	8	1	11	52	64	3FFH	1023
long double	10	1	15	64	80	3FFFH	16383

3.浮点数的规格化

​ 对于一个小数段frac，可解释为描述小数值 f，其中 0≤f<1，其二进制表示为 0.fn-1… f1f0，也就是二进制小数点在最高有效位的左边。有效数字定义为 M=1+f。有时候，这种方式也叫作隐含的以 1 开头的表示法，因为我们可以把 M 看成一个二进制表达式为 1.fn-1fn-2…f0 的数字。既然我们总是能够调整指数 E，使得有效数字 M 的范围为 1≤M<2（假设没有溢出），那么这种表示方法是一种轻松获得一个额外精度位的技巧。同时，由于第一位总是等于 1，因此我们就不需要显式地表示它。拿单精度数为例，按照上面所介绍的知识，实际上可以用 23 位长的有效数字来表达 24 位的有效数字。

​ 比如，对单精度数而言，二进制的 1001.101（即十进制的 9.625）可以表达为 1.001101×2^3，所以实际保存在有效数字位中（即尾数部分）的值为：

00110100000000000000000

即，去掉小数点及其左边的1，并用0补齐尾数（涉及到了补码的位数扩展，详细细节请查阅相关资料）

​ 根据上述规则，下面是将-9.625转化为单精度浮点数的的具体过程：

1、首先，需要将 -9.625 用二进制浮点数表达出来，然后变换为相应的浮点数格式。即 -9.625 的二进制为 1001.101，用规范的浮点数表达应为 1.001101×2^3。

2、其次，因为 -9.625 是负数，所以符号段为 1。而这里的指数为 3，所以指数段为 3+127=130，即二进制的 10000010。有效数字省略掉小数点左侧的 1 之后为 001101，然后在右侧用零补齐。因此所得的最终结果为：

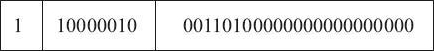
3、最后，我们还可以将浮点数形式表示为十六进制的数据，如下所示：

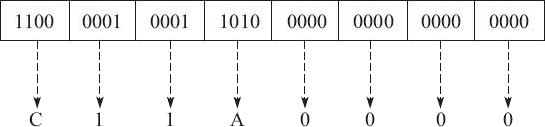
即最终的十六进制结果为 0xC11A0000。

4.揭示特殊值

​ IEEE 标准指定了以下特殊值：±0、反向规格化的数、±∞ 和 NaN（如下表所示）。这些特殊值都是使用 emax+1 或 emin-1 的指数进行编码的。

NaN

​ NaN：当指数段 exp 全为 1 时，小数段为非零时，结果值就被称为“NaN”（Not any Number），如下图 所示。

​

一般情况下，我们将 0/0 或:

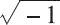
视为导致计算终止的不可恢复错误。但是，一些示例表明在这样的情况下继续进行计算是有意义的。这时候就可以通过引入特殊值 NaN，并指定诸如 0/0 或

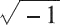
之类的表达式计算来生成 NaN 而不是停止计算，从而避免此问题。下表中列出了一些可以导致 NaN 的情况。

无穷

​ 无穷：当指数段 e全为 1，小数段全为 0 时，得到的值表示无穷。当 s=0 时是 +∞，或者当 s=1 时是 -∞。如下图所示。

无穷用于表达计算中产生的上溢问题。比如两个极大的数相乘时，尽管两个操作数本身可以保存为浮点数，但其结果可能大到无法保存为浮点数，必须进行舍入操作。根据IEEE标准，此时不能将结果舍入为可以保存的最大浮点数（因为这个数可能与实际的结果相差太远而毫无意义），而应将其舍入为无穷。对于结果为负数的情况也是如此，只不过此时会舍入为负无穷，也就是说符号域为1的无穷。

非格式化值

当指数段 exp 全为 0 时，所表示的数就是非规格化形式，如图 5 所示。

在这种情况下，指数值 E=1-Bias，而有效数字的值 M=f，也就是说它是小数段的值，不包含隐含的开头的 1。

非规格化值有两个用途：

• 第一，它提供了一种表示数值 0 的方法。因为规格化数必须得使有效数字 M 在范围 1≤M<2 之中，即 M≥1，因此它就不能表示 0。实际上，+0.0 的浮点表示的位模式为全 0（即符号位是 0，指数段全为 0，而小数段也全为 0），这就得到 M=f=0。令人奇怪的是，当符号位为 1，而其他段全为 0 时，就会得到值 -0.0。根据 IEEE 的浮点格式来看，值 +0.0 和 -0.0 在某些方面是不同的。

• 第二，它表示那些非常接近于 0.0 的数。它们提供了一种属性，称为逐渐下溢出。其中，可能的数值分布均匀地接近于 0.0。

下面的单精度浮点数就是一个非格式化的示例。

它被转换成十进制表示大约等于 1.4×10-45，实际上它就是单精度浮点数所能表达的最小非格式化数。以此类推，格式化值和非格式化值所能表达的非负数值范围如下表所示。

六.小小的总结

​ 通过学习IEEE754标准后，再回顾float.h,相信对一些宏定义的值就有了比较好的理解了，例如

#define FLT_DIG          6                       // # of decimal digits of precision
#define DBL_DIG          15                      // # 转换成十进制形式后，小数点后精确数字（能够保证精度的数字）的位数。

因为单精度浮点数的尾数有23位，2^23 = 8388608，一共七位十进制数，这意味着转化为十进制之后，最多能有7位有效数字，但绝对能保证的为6位，也即float的精度为6~7位有效数字。双精度浮点数同理。

• 本文作者： 迪丽惹Bug
• 本文链接： https://lyroom.github.io/2023/01/12/细说浮点数/
• 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！